前言（阅读指南）

我准备写一个轻松的PCA算法的教程。传说中的零基础教程，也就是不用带特别多脑子去阅读的教程。不过有很好线性代数基础的同学可能会觉得我有点啰嗦。那些超级简单的内容请跳过去就好啦。

问题出发：如何给数据降维

现在我们都知道，PCA（主要成分分析）是一种可以把高纬度的数据降低到低纬的一种降维算法。他的英文全称Principal components analysis。当然你肯定不在乎，全称。我们知道在进行学习机器学习或者流形学习中，样本数据的特征值可能多到可怕(当然有的时候纬度太少可能啥也做不了)，那么这个时候做算法的科学家们就不开心了，这么多纬的样本数据老子玩不来啊。这尼玛算法收敛要几年啊，cpu吃不消。我就一台xp的PC，宝宝心里苦啊。

于是这群傲娇的科学家，就在思考这样一个问题，可以给数据降维吗？

从经验中思考

辛辛苦苦发掘的特征值，你说降维就给我删除了，那怎么行呢？降维要基本法的。可是这样的规律是什么呢？我们先举一个有意思的例子，我要使用纯色的小球体模拟三维空间中的实体，我给出一组采样特征值你看看那个可以不要。（不要考虑这个想法有什么应用，我随便想的）

1	(颜色rgb，灰度值，半径,球体表面积，球心坐标，球体密度分布，球体质量)

“你给的特征啥子鬼呦！”知道了颜色的rgb不就可以模拟出他的灰度值吗！知道了半径，不就知道了表面积吗！知道了半径和密集分布不就知道了质量了吗！……

等下！我们刚才的过程不就是一种降维吗！这里科学家有这更加深刻的体悟（一套自己的话语体系），他们使用什么词汇来描述呢？线性相关性。如果两个特征值的线性相关性越强，那么我们就越有把握把两个特征合并成一个特征。

那么从反面来看这个问题，我们要使降维后的数据越线性不相关越好，因为这样可以保留最多的源数据的信息。

你或许会开始问一个严肃的问题：怎么取衡量降维后的数据的线性相关程度？我们有数学工具方差。也就是说我们要使降维后的数据方差最大。

还记得方差吗？请先回忆起期望。一组数据的期望可以看成他们的平均值，然后方差可以反映数据到这个平均值的波动情况。现在我们要做的就是让这个波动保持最大。

从简单开始：二维到一维

那么我们不妨把先看看数据从二维下降到一维的情况。

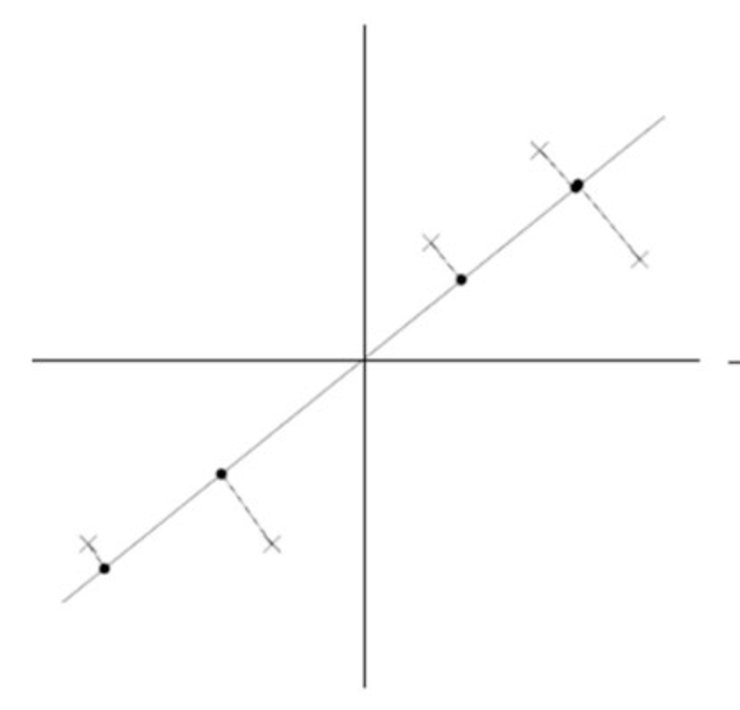
我们的思路是这样的，在平面内过数据的中心点画一条直线，然后让数据向这条直线上投影，可以知道每个点的投影到中心点的距离，使用者个距离作为每个数据的新的坐标。这样就从二维下降到一维了。而且我们也可以计算这里新数据的方差了。

对于m个点的数据中心值，就是各个特征的平局值 $\frac{1}{m}\sum_{i=1}^m x_i$

可是这样的话，计算有点复杂。我们对数据进行一波预处理，把他的中心点移动到原点。（这个过程叫做特征方差归一，或者均值归0化）这样做的好处是现在过原点做任何一条直线，现在投影到这个条直线上的新数据的均值（期望）是0了。这样计算就简单了许多。

如果用图像表示就像下面这样:

推广到高纬度

聪明的你发现了，在三维中我先移动中心点，然后在选取两条过原点的直线做投影就可以啦。那么从a维度下降到b维度，就可以都这么做了。

公式推导

现在有m个样本数据，每个数据有n个特征，即源数据维度为n维。现在要将数据下降到d维度。假设现在数据已经被我们均值化了，就是中心点已经移动到了原点。现在对我们来说最重要的就是求得出使新数据方差最大的那条直线的单位方向向量。（因为肯定过原点了嘛）

于是乎我们做投影表示数这当中一天直线上投影数据的方差。如下图。

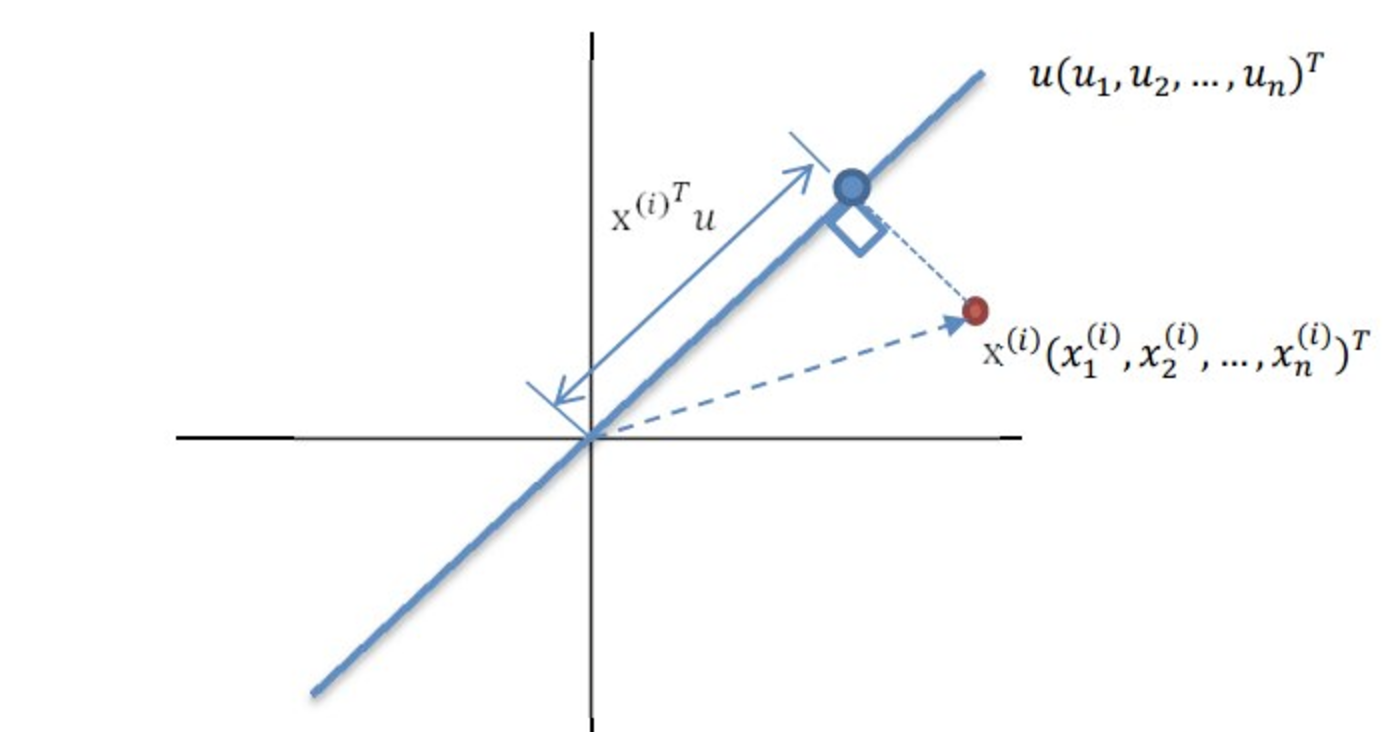
其中$ x^{(i)} $表示的是第i个元素。

现在不难得出方差:(一会就知道我为什么要使用符号 $ \lambda $)

$\lambda = \frac{1}{m} \sum_{i=1}^m \big( {x^{(i)}}^T u \big)^2$

在这里我们可以发现：

${x^{(i)}}^T u = u^T x^{(i)}$

现在仅仅把平方中的一个换成另外一个整理后就可以得到下面的公式了：

$\lambda = u^T \bigg( \frac{1}{m}\sum_{i=1}^{m} x^{(i)}{x^{(i)}}^T \bigg) u$

中间那个大括号里面的是不是很熟悉呢？那现在我这样写呢：

$cov(X,X) = \frac{1}{m}\sum_{i=1}^{m} (x^{(i)}-0)(x^{(i)}-0)^T$

哈哈现在发现了吧，由于我们移动了中心点，E（X）=0；那么原来公式中的大括号中的就是元素数据的本征协方差矩阵。注意这个矩阵是可以求的（而且是方阵）。现在我们令这一大坨为$ \sum $
然后我们等式两边都去左乘u,然后就会得到：

$u\lambda = uu^T\sum u$

由于u是单位方向向量，那么$uu^T=1$于是乎：

$u\lambda = \sum u$

石破天惊

看到上面的式子，真有一种石破天惊的感觉。我差一点哎呀的叫起来。这个不就是矩阵的特征值和特征向量吗！方差就是特征值，方向矩阵就是特征向量。更加诡异的来了。由于特征值的定义，这里面的特征向量是相互正交的。也就是说：

我们得到了一组符合条件的正交基

不知道你还有没有印象了。线性代数中正交变换，可以使用过渡矩阵，仅仅做一次矩阵间乘法就可以了。现在为了保证方差最大，我们仅仅要对得到的方差进行排序。然后降到几位就取前几个作为正交基就可以了。

到了这里没有什么好讲的了，都是线性代数书上已经写的很好的东西了。

后记

注意这里面降维后的数据，保留了一定的源数据信息，但是现在不能说原来的某个特征就到了某个新的维度上，仅仅是点有一对一的关系。

PCA算法可以说是出奇的优雅，核心思想过程很简单，推导也不需要很高的数学基础，不过要是没有学习过线性代数的话，不会突然有震撼感。真不知道，算法作者到底是从正交基想到了可以去降维，还是通过想要降维，推导到了线性代数里的正交基呢。也可能是两个思路同时进行，突然有一天一切都联通了。神奇了。

当然，最大方差不是唯一的解释这个算法的思路还有其他的解释。欢迎补充交流，指正错误

我将一直迷惑和无知，我是黄油香蕉君，再见