前言
人类的智慧是无限的。当我看到了下面的证明之后我相信了这一点。希望你也可以体会到我所感受到的震撼。
命题
在6个人的聚会中,一定有三个人互相都认识,或者三个人互相都不认识。
现在想想怎么证明。或许你和我一样一开始想到的是条件概率,贝叶斯公式。这样也不是证明不出来,而是证明的方法显的暴力,和不用脑子。有一种极其优雅的证明。现在验证你是不是天才的时候来了,关掉这个博客,然后思考两天。对比一下你的证明方法。
两天之后
现在我可以解开谜底了。
我们现在来转换一下命题,看看他在等价命题是什么。首先有6个人,我们可以理解为6个ABCDEF。然后每两个人之间的关系使用连线表示,我们规定如果两个人认识,我们使用红线连接,如果两个人不认识使用蓝线连接。现在我们要证明的是6个点互相连线的图像,对边进行红蓝任意的上色,其图形中必然存在一个全色三角形。
好了!现在是不是觉得豁然开朗了呢?请开始你的证明吧。再给自己两天时间如果证明不出来,再来看看下面的结果。
又两天之后
证明:
现在考虑一个点和其他剩下5个点的关系。根据抽屉原理这5个点中必然有3个的边是同样颜色的。(关于这个你可以自己动手试试,或者试着推导,还可以百度哦!)于是我们把这个四个点抽象出来。令他们为abcd。如下如所示:
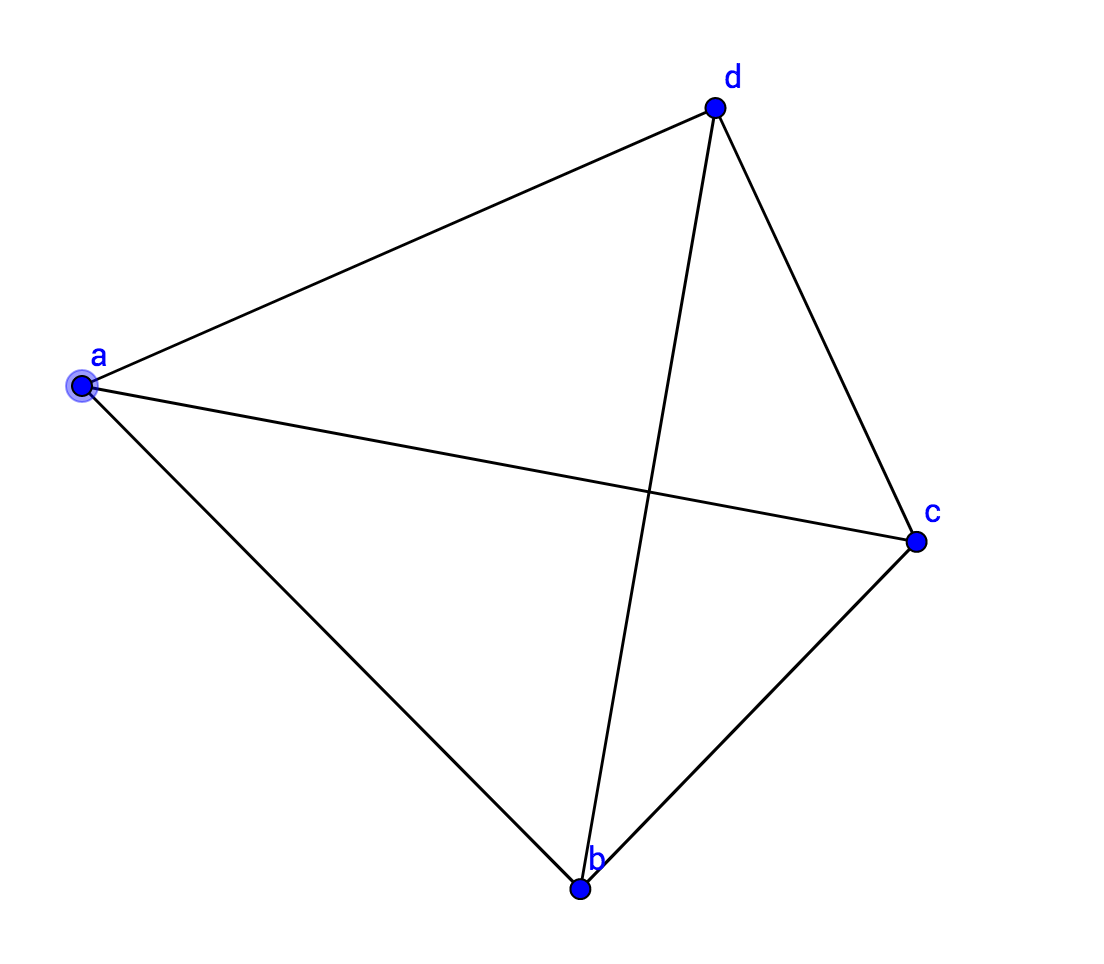
现在已经知道,ab,ac,ad都是一种颜色的,不妨令它为红。现在看看三角形bcd。发现如果其中一条边是红色的,那么图形中必然有一个全红的三角形。如果全都不是红色的,bcd就是一个全蓝的三角形。证明完毕!
More
同学,我们似乎是接触到了一门很有趣的知识。拉姆齐定理。这里有维基百科的传送门。这也是为什么我的标题中使用了R(3,3)的原因。
我将一直迷惑与无知,我是黄油香蕉君,再见。
