总前言

以前在自学机器学习的时候，只是简单的看了一下思路然后就是跟着进行数学推到。至于从算法到实际实现总是存在一些距离。于是就有了自己写这样一系列文章的想法。就是把自己从知识到实践的过程记录下来。思考出一条从理论到实践的路径。这一直都是我非常想研究的。一篇文章或许看不出什么，不过我相信只要坚持这种工作，一定可以得出令人欣喜的答案来的。

简介

Mean shift 中文译名又叫做，均值漂移。在机器学习领域可以实现聚类，在图像领域可以实现目标追踪，和图像平滑。是一种应用很广的算法。接下来我将尝试使用通俗的语言，在不借助数学工具的情况下使你了解这个算法都做了什么。

算法思想

二维空间

首先我们先假设一个任务。我们给出平面中的一组点，然后要求你根据这些点的信息，将空间分割开来。怎么分割呢？如果给你一只铅笔，你或许可以把这些点想象成天空中的星星，有的地方很密集，有的地方和稀疏，有的像星云的一部分，有的又像银河之类的一个尾巴。你可能凭感觉画出来了。但是这样的工作可以由机器自动完成吗？
答案是可以，我们选取平面内的任意一个点，看看他周围已经存在的数据对这个点的影响是什么。然后通过这个影响移动这个点。然后在进行迭代，就可以得出这个点收敛的数据了。(收敛的条件当然是这个影响趋近与0)
额。听起来还是很抽象？看看下面的图片你就明白了。

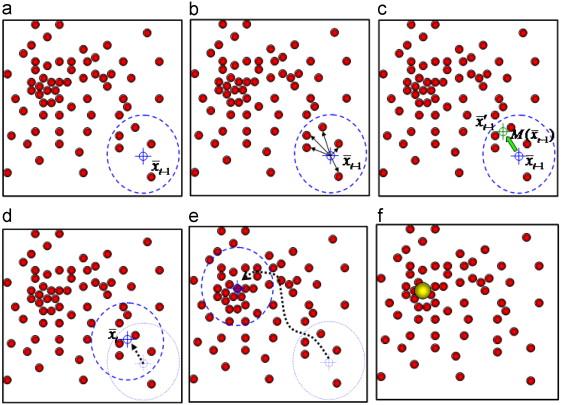
首先先随便选取一个点X，然后画一个半径为h的圆。之后求在这个圆中(圆形内部)的点到X所构成的向量的和。我们称之为平均向量。
之后对X在平均向量上的方向和距离上进行平移。得到新的X。然后重复这个步骤。一直到它附近的点的平均向量为0，或者长度足够小。（小于我们设定的值）
注意,这个时候，如果你是要分割平面，你要想象许多的点，把平面内的位置都覆盖了，你会发现最后所有的点也就只收敛于几种值。如果你要对已经有了的点进行聚类，那么你就只需要把要分类（实际是聚类）的点都进行一次计算就可以了。（这里有个小技巧，理论上在计算过程中所有经过的点，和包裹到的周围的点都可以认为是一个类别里的，这样在一些时候可以大大减少计算的量。）

三维空间

如果二维空间内的点的移动方法和规律你已经理解了，那么不难推广到三维的空间中。这里只要把原来用于圈住周围点的圆，变为球体就可以了。下面我给你看一张在mean shirt论文里面在三维空间进行聚类的结果图。

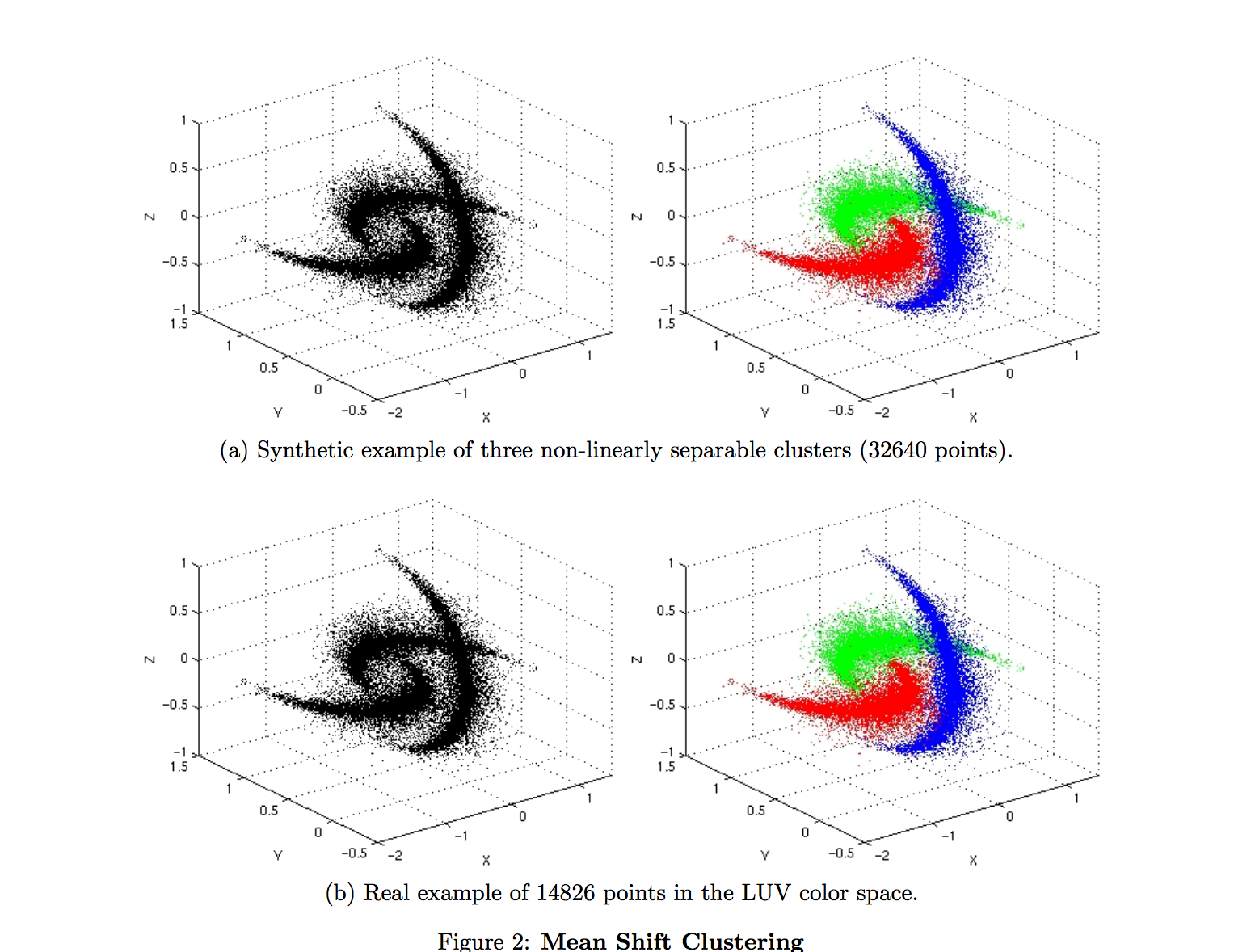
怎样很神奇吧，这些3维空间中的点被分为了三类。现在闭上眼睛好好想象一下，这些点不断的画球移动然后停在一个点的过程。

推广到高维

和刚才过程一致。现在把球体，改成超球体即可。什么是超球体呢？你可以理解为无论从那个维度对他进行投影都是一个圆就可以了。不用强迫自己完全想象出来。

这里的描述不够准确，应该是说投影到任意的二维空间中是一个圆。投影到任意三维空间是球体。感谢。@申波同学的帮助。

公式推导

或许你觉得低维度下，很好思考和实现，但是数学家们，或者玩算法的人希望自己的算法是万能的。于是我们要借助数学工具对算法进行推导，和重新表述。不要害怕!这个和我刚才说的，并没有多大的不同。现在你要做的就是理解，每一个步骤，然后在不懂的地方停下来思考一下就行了。

基本形式

在给定的 $ d $ 维的空间 $ R^{d} $ 中有 $ n $ 个样本点。这样不难得出在空间中任意一个点的Mean shrift向量如下：

$M_h = \frac{1}{K} \sum_{x_i \in S_k} (x_i - x)$

简单的解释一下这个公式。$ K $是指的是$ x $有$ K $个临近点。其中超球体$ S_k $的半径为$ h $,它的公式表示如下:

$S_h = \{ y:(y-x_i)_T(y-x_i) < h^2 \}$

使用核函数进行密度估计

首先我把这个密度估计的函数给出来:(注意这里面$ K() $是核函数)

$f(x) = \frac{1}{nh^d}\sum_{i=1}^nK(\frac{x-x_i}{h})$

你或许会问这个是什么玩意？我为啥要密度估计？还有你为啥知道密度估计是这公式呢？

现在我们开始以二维的数据进行思考。想象一下一个平面上面有许多的点我们可以用(x,y)来表示。现在我们要通过平面内现有的点的疏密来获取平面上每个点的密度值。于是原来的（x,y）变成了（x,y,z）。他是一个表示平面内每一个点密度的曲面。就像下面这个图一样。

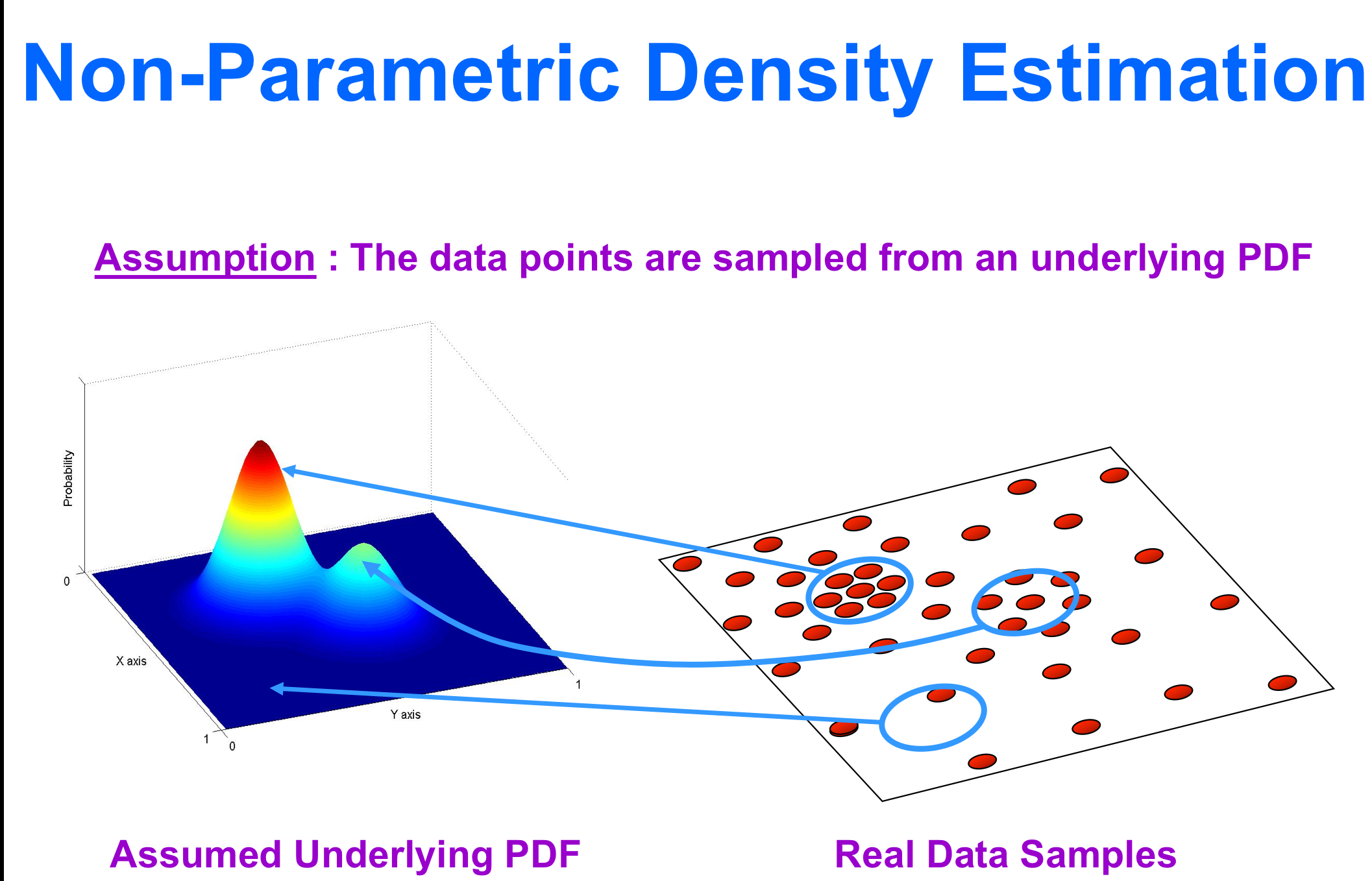
看到了这个密度曲线你是不是豁然开朗了。如果你还没有感觉，不妨想象一下把左边的那个“小山脉”倒置过来，就成了一个小漏斗。现在吧一个小球放在任意一个点上，小球滚动后，必然的停止在一个“小山”的“顶峰”。这就是模拟了上面“向量漂移”的动作。（使用模仿这个词不太恰当）哦!现在对这个密度函数求偏导数，然后命令其等于0就可以知道哪里是“山峰”了，因为“山峰”是平的。(偏导数应该为0)

“等等，不要蒙我！”你或许会说。这里没有解释两点，1.为什么原来的点是离散的，现在就变成连续的曲面了呢？2.这里和核函数有什么关系呢？

好吧。在求取偏导数之前。我来尝试解释一下这个问题，不过这里只不过是我的一种理解方式。首先一个离散的一维的点的密度怎么表示呢？我们知道点在总个数为N。于是我们不妨选取一段很小的距离h，然后看看在这段范围内有多少的点。假设有k个点。于是他的密度可以近似的表示为：$ p = \frac{k}{N} $,想象一下这里面h足够的小，然后我们可以得到这样的图像。

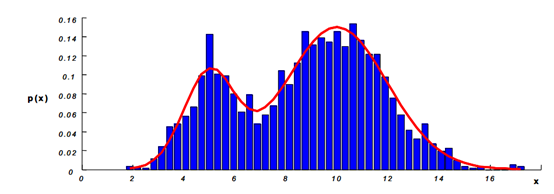
现在再想想$ \frac{k}{N} $是点出现的概率，并不是在真正的密度，思考在二维空间中，真正的密度应该是$ \frac{k}{NV}$ 其中V可以理解为一个以h为边长的正方形。我们便可以说这里的h是窗口的大小。
可是现在表示整个密度的函数似乎太麻烦了。那怎么办呢？我们设想一个辅助函数。让他有下面三个功能：

在窗口内有值，在窗口外没有值。
这个函数表现出离x越近对密度的结果影响越大，越远越小。
函数在各个方向上的影响是一致的。（对称的）

细心的读者或许会发现条件2其实包含了条件1。没有值可以理解为对结果的影响为0。

现在我们就给自己投机取巧的函数起名为K，于是就可以轻易表示出来在二维空间中的密度函数。

$f(x) = \frac{1}{nh^2}\sum_{i=1}^nK(\frac{x-x_i}{h})$

这里我关于使用$ \frac{x-x_i}{h} $中的h是这样理解的。这的距离尺度是相对于窗口大小h的距离。而不是绝对距离。这在一维的空间可以理解为距离，而在二维就是一个向量了。所以这里的解释可能存在一定的问题。希望读者，有更好的解释可以，告诉我。谢谢您 :）

怎么样？现在这个公式是不是和之前的很像了。除了这里的是2维的d=2.现在推广到d维，就可以得到我们要的公式了。但是你仍然不满足：“你怎么知道有这样的函数K，正好满足你的种种变态要求呢？”。你别说还真有，而且还很多。

那他们张什么样呢？为什么又这些神奇的功效呢？了解更多请使用传送门。我可以先截一张图，让大家感受一下，这里不做过多的介绍了。

注意这里有关于核函数的还有:传送门这个是介绍SVM（支持向机）中的核函数。但是我对于核函数的理解还不是很深。希望哪位朋友有相关论文或者文章推荐给我。万分感谢。

开始纯数学推导吧！

首先要确定核函数的公式。

$K(x) = c_{k,d}k(\|x\|^2)$

将核函数代入到原来的密度估计公式，然后求梯度得到$ \nabla f(x) $。之后令$ \nabla f(x) = 0 $这是接上面提到的大体的思路。

$\nabla f(x) = \frac{2c_{k,d}}{nh^{d+2}}\sum_{i=1}^n(x_i-x)g\big( \big\|\frac{x-x_i}{h}\big\|^2\big)$

其中$ g(s) = -k’(s) $。这里来简单的理解一下，注意这里我们求的是密度估计函数的梯度，于是这里反应的是梯度下降的最快方向了。那么我们仔细观察上面这个公式，是不是有点意思了！

$\frac{2c_{k,d}}{nh^{d+2}}$

不过是一个常数，我们先忽略他。然后看看

$\sum_{i=1}^n(x_i-x)$

是不是突然想哭出来？这个不就是那个各个点到x的向量和吗！

$g\big( \big\|\frac{x-x_i}{h}\big\|^2\big)$

一看就更加的亲切了，这个不就保证了在窗口h内有值在窗口h外对梯度下降的影响是零吗！更加神奇的是你发现里x越近的点在对$ (x_i-x) $这个向量的加权越大（特别在高斯核下,在别的核下可能加权是一样的）。
现在回忆一下前文，我是不是说过的“模仿”一词不准确？对，这里是向量的漂移模仿了，梯度函数求极值点的过程。而且正好描述的是在核函数影响下窗口大小h内点权重一致的情况。
现在我们知道了我们要在$ \nabla f(x) $下求极值点。那就可以使用最传统的方法，求出一个点的梯度，然后按照梯度的方向移动一段距离，再继续求梯度。重复这个过程，一直到求出的梯度趋近于0。现在便知道了这个方向是:在窗口h内的点到x所构成的向量的加权和。看看我们终于回到了最初的定义了！

但是向这个方向移动多少呢？步子迈大了容易扯到蛋（移动过了，然后来回摆动永远不收敛），步子迈小了收敛速度太慢了。那么可不可以让在它在离收敛点远的地方，步子大一点，接近了极值点，步子就小一点呢？
答案是：当然可以！

自适应步长

我们在来回顾一下，这个公式。请始终记住他表示的是密度函数的梯度。下降最快的方向。

$\nabla f(x) = \frac{2c_{k,d}}{nh^{d+2}}\sum_{i=1}^n(x_i-x)g\big( \big\|\frac{x-x_i}{h}\big\|^2\big)$

现在对这个公式进行一定的整理。后得到：

$\nabla f(x) = \frac{2c_{k,d}}{nh_{d+2}} \bigg[ \sum_{i=1}^n g \bigg( \bigg\|\frac{x-x_i}{h}\bigg\|^2\bigg) \bigg] \bigg[ \frac{\sum_{i=1}^n x_i g\big( \big\| \frac{x-x_i}{h}\big\|^2\big)}{\sum_{i=1}^n g\big( \big\| \frac{x-x_i}{h}\big\|^2\big)}-x \bigg]$

没看出来怎么推导出这部的同学请来看 ：关于这个公式很多的同学表示很头大，但是如果你看完我的介绍，可能会吐血哭出来。这个就是简单的分数运算。首先把$ x-x_i $和后面的一大坨乘开。然后在每一项在除以那一大坨。在外面乘以那一大坨。就是这个公式了。

关键的地方来了。注意理解这个公式。现在我们令$ G(x) = c_{g,d}g(| x |^2)$,那么这时第二项，就变成了对于新核函数G(x)进行的密度估计。好！停下来思考两秒钟。

那么这个第二项就是一个大于0的数了。于是乎我们令第三项为$m_h$。仔细思考一下这个$m_h$就是我们要的自适应的步长。

$m_h(x) = \frac{\sum_{i=1}^n x_i g\big( \big\| \frac{x-x_i}{h}\big\|^2\big)}{\sum_{i=1}^n g\big( \big\| \frac{x-x_i}{h}\big\|^2\big)}-x$

思考一下你会发现，由于第一项和第二项是一个数不对这个梯度变为0提供贡献，所以这一项可以提供梯度下降的方向。然后我们看到

$\sum_{i=1}^n g\big( \big\| \frac{x-x_i}{h}\big\|^2\big)$

是核函数密度的估计，以高斯核为例，这里原来的密度估计完全一致。也就是说，这里的$m_h$和原来的密度估计成反比，这样就做到了密度大的地方，他的倒数就小。密度小的地方他的倒数就大。
于是反应到步长上就是，离模点（极值点）远的地方，步长大，近的地方步长小。

$x' = x + m_h(x)$

这个就是可以使用算法迭代的最终公式。顺便提一句这里$m_h$就是人们口中的mean shift向量了。

写在最后

终于完成了。不知道你理解了没有。我没有读过研究生，或有专业老师的指导，如果有什么错误，欢迎指正。感谢你的阅读。

我将一直的迷惑和无知，我黄油香蕉君，再见。